在2018年4月17日上午11:03,金属疲劳导致西南航空1380次航班(从纽约飞往达拉斯,飞行高度32,000英尺)左侧引擎内部的一个风扇叶片断裂。断裂炸开了引擎外壳,金属碎片撞击机身,击碎了14排的一个窗户。随之而来的急速客舱减压导致一名乘客被吸出受损的窗户半个身子,并受到致命伤。飞行员成功地在费城安全降落飞机,避免了更大的悲剧。
多年来,由金属疲劳引起的飞机事故数量一直在稳步增加,在最近统计的2010年代达到高峰,为30起。其中几起事件严重到需要紧急迫降。虽然2024年1月波音737 Max 9飞机门塞在16,000英尺高空脱落事件可能是由于螺栓缺失,但Max系列飞机在2019年曾发生过一起与疲劳相关的安全问题,当时易发生裂缝的机翼前缘缝翼不得不更换。
飞机被形容为“两百万个零件组成的密集编队飞行”,很多地方都可能出错。连续的飞行使这些零件经受强烈的应力和松弛循环,在此期间,制造过程中不可避免的小缺陷可能导致微小的裂缝。一旦裂缝长到足够长,就像西南航空1380次航班的风扇叶片底部发生的那样,相邻的部件可能会断裂脱落。因此,飞机设计师需要预测部件必须承受的最大应力。
支持科学新闻报道
如果您喜欢这篇文章,请考虑通过以下方式支持我们屡获殊荣的新闻报道 订阅。通过购买订阅,您正在帮助确保有关塑造我们当今世界的发现和想法的具有影响力的故事的未来。
裂缝可能出现在像大坝、桥梁和建筑物这样巨大的结构中,也可能出现在像我们自己身体里的骨骼和牙齿这样生物学上密切相关的结构中。例如,美国国家标准与技术研究院的工程师正在对2021年佛罗里达州海滨公寓的倒塌事件进行建模,以了解支撑结构中的裂缝可能在灾难中起到的作用。最近对在北大西洋内爆的泰坦号潜水器的分析已经确定了可能发生断裂的区域。在金属、混凝土和牙釉质中,裂缝形成于承受最大应力的区域——当裂缝超过临界长度时,它们可能是最危险的,而临界长度取决于材料。
工程师可以使用类似的工具来研究各种各样的裂缝并防止故障。作为防止故障的重要防御措施,机器或结构应进行物理测试,但这种测试可能很昂贵,并且可能并非总是可行。一旦部件投入使用,就应定期检查,这也非常昂贵。
除了这些实践策略之外,还有防止故障的第三个关键方面:计算机模拟。在开发过程中,模拟有助于工程师创建和测试在许多不同条件下应保持可行的设计,并且可以针对强度和重量等因素进行优化。例如,飞机需要尽可能轻便耐用。如果操作得当,模拟可以帮助防止事故发生。
随着美国启动大规模的基础设施改造计划,提高计算机模拟的可靠性可以帮助确保安全。
这些模拟的可靠性对于安全至关重要——但它们没有像制造缺陷、维护错误或检查频率那样受到同样的审查或监管。分析1991年挪威石油平台倒塌事件的工程师发现,由于模拟错误,其中一个内部支撑墙的预计应力仅为实际应力的一半左右。因此,它的设计加固比需要的要轻得多,结果就失效了。
随着美国启动大规模的基础设施改造计划,确保安全性和耐久性将至关重要。可靠的计算机模拟可以帮助实现这两者,同时减少对昂贵的物理测试的需求。然而,令人担忧的是,工程师使用的模拟通常不如它们需要的那样可靠。数学正在展示如何改进它们,从而使汽车、飞机、建筑物、桥梁以及其他物体和结构更安全且更便宜。
考虑到21世纪机器的复杂性,17世纪70年代发布的字谜竟然是其力学的基础,这真是令人好奇。被称为胡克定律的ut tensio, sic vis(“伸长量与力成正比”)指出,弹性物体(如金属弹簧)的形变与施加在其上的力成正比。只有当物体保持弹性时,该定律才仍然有效——也就是说,如果当力移除时,物体恢复到其原始形状。当力变得过大时,胡克定律不再适用。
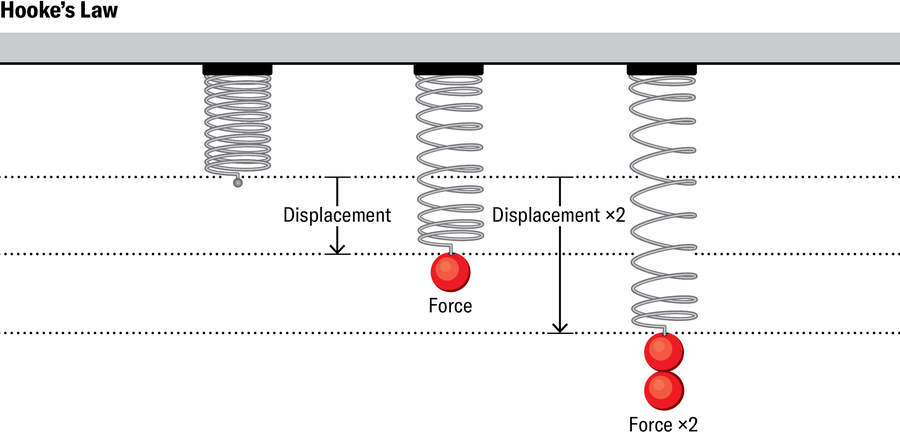
珍·克里斯蒂安森
在更高维度中,情况变得更加复杂。想象一下轻轻按下粘在桌子上的橡胶立方体。在这种情况下,立方体的高度与其原始高度相比的减少量,即“应变”,与您施加在立方体顶面单位面积上的力,即“应力”成正比。人们还可以以不同的角度对不同的面施加不同的力——用工程师的话说,让立方体承受不同的“载荷”。然后,应力和应变都将具有多个分量,并且通常会逐点变化。胡克定律的广义形式仍然成立,前提是载荷不要太大。它表示应力和应变仍然成正比,尽管方式更复杂。例如,将所有应力加倍仍然会使所有应变加倍。
人们使用胡克定律来分析各种各样的材料——金属、混凝土、橡胶,甚至骨骼。(该定律适用的力范围取决于材料的弹性。)但该定律仅提供了确定物体将如何响应实际载荷所需的多条信息之一。工程师还必须考虑作用在物体上的所有力的平衡,包括内部和外部力,并指定应变如何与不同方向的变形相关联。最终得到的方程称为偏微分方程 (PDE),它涉及诸如应力和应变等量在不同方向上的变化率。它们过于复杂,无法手工求解,甚至无法精确求解,特别是对于在风扇叶片和桥梁支架等中遇到的复杂几何形状。
即便如此,最值得注意的是,从1967年弗拉基米尔·孔德拉季耶夫开始,数学家们已经分析了这些 PDE 在常见几何形状(如多边形和多面体)中的应用,以获得有价值的见解。例如,应力通常在任何角和边缘附近最高。这就是为什么如果您先切开一个小口,然后从切口处开始拉开箔纸,就更容易撕开一张箔纸。
问题在于,许多对其完整性对于安全至关重要的机器零件在其设计中都包含了此类特征。虽然角尖和边缘通常会尽可能地倒圆,但裂缝仍然更容易在这些地方形成。将边界两侧直接拉开的载荷最有可能扩展裂缝。因此,工程师必须特别注意这些位置以及作用在它们周围的力,以确保物体在开始破裂之前能够承受的最大应力不超过极限。
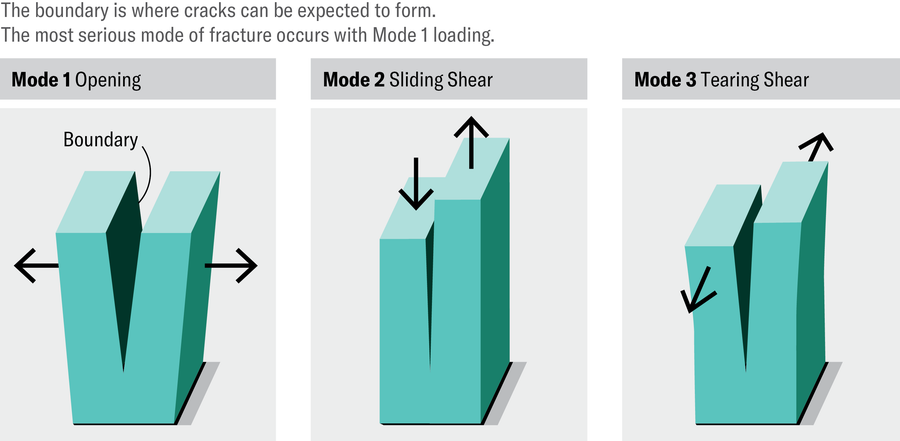
珍·克里斯蒂安森
为了做到这一点,他们需要找到在各种实际载荷下物体 PDE 的近似解。工程师有一种方便的技术来实现此目的,称为有限元 (FE) 方法。在1956年一篇具有里程碑意义的论文中,工程师 M. 乔纳森·特纳、雷·W·克拉夫、哈罗德·O·马丁和 L. J. 托普指出,为了理解物体如何变形,将物体视为由许多连接的部分组成(现在称为有限元)会有所帮助。
假设您想找出当强大的风垂直吹袭二维弹性物体(例如沿其周边固定的绷紧屏幕)时,该物体会如何变形。想象一下,用一堆连接的三角形面片代替屏幕,每个面片都可以移动和拉伸,但必须保持平坦的三角形。(也可以使用四边形。)这种由三角形制成的模型屏幕与原始光滑屏幕不同,但它提供了一个更容易处理的问题。对于实际屏幕,您需要找到每个点的位移——这是一个无限的问题——对于由三角形制成的模型屏幕,您只需要找到每个三角形角的最终位置。这是一个有限的问题,相对容易解决,并且屏幕表面的所有其他位置都可以从其解中推导出来。
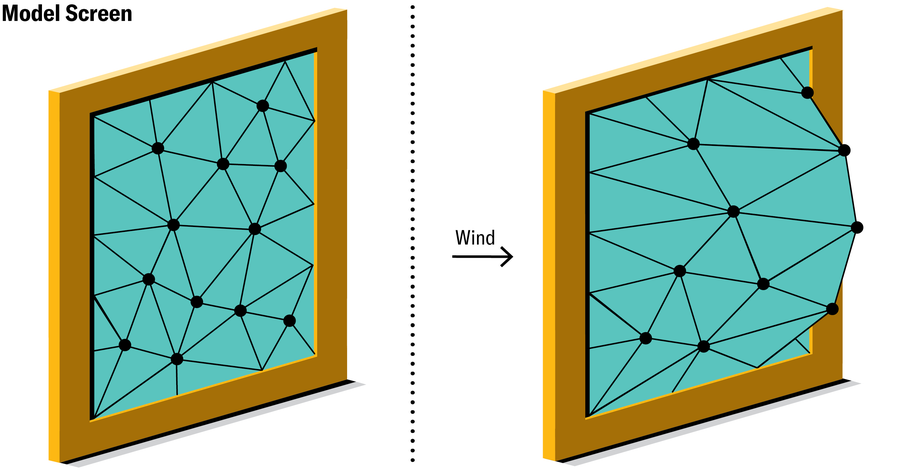
珍·克里斯蒂安森
物理学中的一个支配原则指出,屏幕将呈现出势能最小的形状,这是它因其位置或配置而拥有的能量。同样的原则预测,吉他弦被拨动后,最终将恢复到直线形状。该原则也适用于我们简化的有限元屏幕,从而产生一组相对简单的“线性”方程,用于求解节点处的未知位移。计算机非常擅长求解此类方程,并且可以告诉我们模型屏幕如何变形。
三维物体也可以类似地建模;对于这些物体,有限元通常是块体或四面体,并且方程的数量通常要高得多。例如,对于整个飞机的建模,人们可能会预期一个具有数百万个未知数的问题。
虽然有限元方法最初是为确定结构在受力时的行为而开发的,但该技术现在被视为求解 PDE 的通用方法,并且也用于许多其他领域。这些领域包括,例如,肿瘤学(跟踪肿瘤生长)、制鞋业(实施生物力学设计)、电影动画(使运动更逼真,如 2008 年的皮克斯电影机器人瓦力)和乐器设计(考虑振动的影响在乐器内部和周围)。虽然有限元对于大多数人来说可能是一个陌生的概念,但人们很难找到一个我们的生活领域没有它们发挥作用的地方。
一些应用涉及裂缝建模。例如,2018年研究的作者使用有限元来探索裂缝如何在牙齿中扩展以及哪种修复体可能最有效。在另一项研究中,科学家们研究了骨质疏松症可能导致不同年龄段的哪些类型的股骨骨折。有限元模拟还有助于在故障发生后揭示根本原因,例如佛罗里达州公寓倒塌和泰坦号内爆,并且在飞机事故后是常规操作。
凭借他们积累的经验,工程师理查德·H·麦克尼尔、约翰·A·斯旺森、佩德罗·V·马卡尔和其他人在 20 世纪 70 年代发布了几个商业有限元代码。其中最著名的“传统”代码最初是为 NASA 在 20 世纪 60 年代后期编写的,现在被称为开源 NASTRAN(“NASA 结构分析”的缩写)。NASTRAN 仍然是航空设计关键步骤的首选程序,工程师在其中对正在设计的整个飞机的计算机模型进行粗略的有限元分析,以识别最有可能发生结构问题的区域和部件。然后对这些区域和部件进行更详细的单独分析,以确定它们将承受的最大应力以及裂缝可能在其中如何扩展。
诸如螺栓是否可能断裂或风扇叶片是否可能断裂等问题在单个部件层面上得到解答。几乎所有此类局部分析都涉及几十年前推出的传统程序,因为它们在商业环境中占有很大的市场份额。我们乘坐的飞机或驾驶的汽车中最终使用的成品零件的设计在很大程度上取决于这些代码。工程师能够从它们那里获得的答案有多准确?为了找出答案,我们需要深入研究数学。
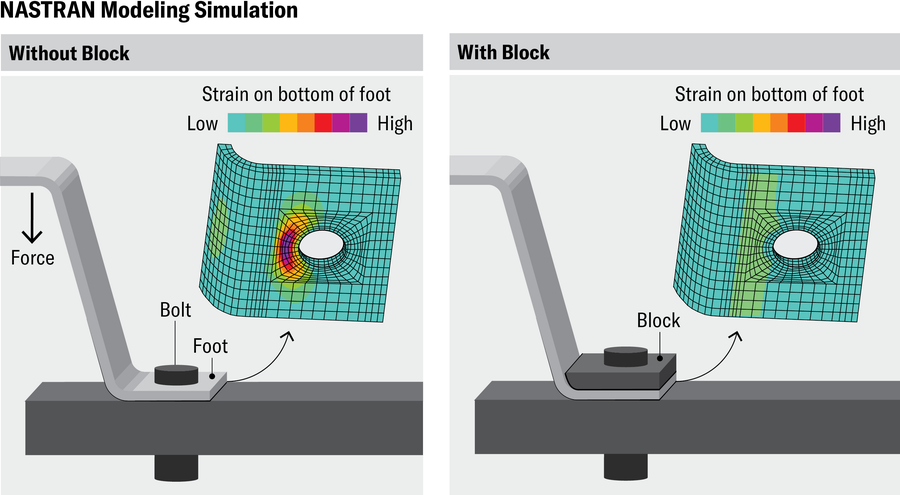
珍·克里斯蒂安森;来源:Robert J. Wingate 的“马歇尔航天飞行中心用于研究航天飞机外储箱纵梁故障原因和纠正措施的应力分析和测试”,第 53 届 AIAA/ASME/ASCE/AHS/ASC 结构、结构动力学和材料会议论文集,2012 年 4 月(参考文献)
早些时候,我们了解了如何确定屏幕的有限元模型的变形,但是这个结果与真实变形有多接近呢?法国数学家让·塞阿在他的 1964 年博士论文中首次提出的一个非凡定理,但根植于俄罗斯数学家鲍里斯·G·加勒金的工作,有助于回答这个问题。该定理指出,只要我们最大限度地减少势能,在我们有限元屏幕可以呈现的所有可能变形中,通过我们的方法计算出的变形将是最接近 PDE 预测的精确答案的变形。
到 20 世纪 70 年代初期,世界各地的几位数学家都使用塞阿定理来证明,随着网格变得越来越精细,元素越来越小、数量越来越多,有限元模型的预测与真实形状之间的差异将减小到零。数学家伊沃·巴布什卡和 A. 卡迪尔·阿齐兹(当时分别在马里兰大学学院公园分校和巴尔的摩县分校)在 1972 年出版的具有里程碑意义的书中首次提出了统一的有限元理论,其中包含此定理和其他基本数学结果。
但在大约同一时间,数学家开始发现工程师正在将各种修改和“技巧”纳入商业代码中,这些代码虽然经常违反能量最小化的关键特性,但在经验上似乎是有效的。麻省理工学院的数学家吉尔伯特·斯特朗将此类修改命名为“变分犯罪”(“变分”来自变分法,变分法与有限元方法相关)。数学家可以证明,其中一些“犯罪”是良性的,但另一些则有可能产生明显不正确的答案。
特别有问题的是用于处理称为锁定的精度下降的变通方法。当基本弹性方程包含一个接近无穷大的值时,就会出现此问题——例如,一个分母中使用极薄金属板厚度的分数。锁定也常发生在橡胶模型中,因为与胡克定律相关的弹性值变得非常大。直到 20 世纪 90 年代,巴布什卡和我才提供了锁定的精确定义和表征。到那时,其他几位数学家,最著名的是意大利帕维亚大学的弗朗哥·布雷齐,已经针对许多问题确定了哪些用于处理锁定的变分犯罪是合理的,哪些应该避免,因为它们可能会给出不准确的答案。
但是,所有这些分析对传统代码几乎没有影响,在传统代码中,有风险的修改仍然存在。原因之一是,当数学家提出修改建议时,这些代码已经根深蒂固,因此将它们纳入其中是不切实际的。此外,数学预测与实际实践之间似乎存在差距——正如德克萨斯大学奥斯汀分校航空航天工程学教授托马斯·J·R·休斯所说,“存在灰色地带”。“一些在数学上可疑的修改在常见问题中可能比经过批准的修改表现更好。”
将更安全的锁定解决方案纳入其中的最大障碍也许是数学和工程学对有限元建模的不同看法。数学家将有限元解视为一系列近似值中的一个,在适当的数学条件下,这些近似值保证收敛到精确解。然而,在工程实践中,有限元建模是一种独立的设计工具,它可以告诉您实际建造的物体将如何表现。普通工程师通常最多在几门课程中学习有限元,通常不会提及诸如问题修改之类的事情。休斯讲述了一个轶事,一家建模公司拒绝购买较新的软件产品,因为其结果与 NASTRAN 给出的答案不符。客户坚持认为 NASTRAN 的解决方案是精确且正确的。(新软件的设计人员只有通过逆向工程新软件,才能使其产生的答案与 NASTRAN 的答案相匹配)
有限元解实际上可能与它们应该预测的物理结果大相径庭。原因包括变分犯罪、基本数学模型的局限性、模拟中排除较小的特征以及使用有限问题代替求解 PDE 的无限问题。例如,大型飞机部件(如机身和机翼)的初步分析就是这种情况。工程师必须使用过去的实验结果来“调整”有限元输出,然后才能弄清楚真实的预测是什么。这种积累的智慧对于解释尚未经过物理测试的新设计的有限元结果至关重要。
较小零件(如耳片和紧固件)的强度分析可能会带来更多问题,因为通常没有可用于调整事物的物理数据。一家大型航空航天公司向四个使用传统代码的承包组织提出的 2022 年裂缝分析挑战问题发现,三组的结果与真实的实验确定解存在显著差异。计算显示裂缝的扩展速度比实际速度慢得多,导致预测的安全裕度令人不安地膨胀。
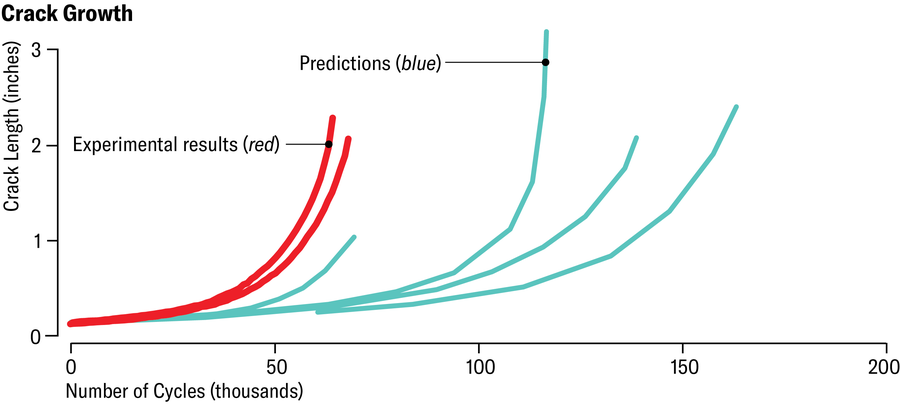
珍·克里斯蒂安森;来源:Barna Szabó 和 Ricardo Actis 的“应用科学中的划界问题”,计算机与数学及其应用,第 1632 卷;2024 年 5 月(数据)
其他此类挑战问题表明,不准确的代码不一定是核心问题——参与者通常会做出无效的简化假设,或者从原始三角形和四边形的众多可用变体中选择了错误的元素类型。此类错误可能会代价高昂:前面提到的 1991 年挪威石油平台倒塌事件造成的损失按今天的美元计算超过 16 亿美元。模拟缺陷也与F-35 战斗机的许多疲劳和裂缝问题有关,这些问题导致其成本严重超支和延误。总的来说,对计算结果的确定性越小,就必须越频繁地进行昂贵的检查。
估计模拟的可靠性的问题似乎令人绝望。如果我们不知道飞机部件等计算机模型的精确解,我们如何才能衡量任何近似解中的误差呢?但我们确实对解有所了解:它满足物体的偏微分方程。我们无法求解 PDE,但我们可以使用它们来检查候选解的效果——这是一个容易得多的问题。如果将未知的精确解代入 PDE,它将简单地产生 0。近似解将产生余数或“残差”,通常称为 R——衡量解的优劣的指标。
此外,由于物体是通过只能以某些方式变形的有限元建模的,因此计算出的应力不会像现实中那样平滑地变化,而是在元素的边界之间跳跃。这些跳跃也可以从近似解中计算出来。一旦我们计算出残差和跳跃,我们就可以使用巴布什卡和匹兹堡大学的沃纳·C·莱因博尔特以及其他数学家在 20 世纪 70 年代后期开始开发的技术来估计任何元素上的误差。从那时起,也开发了其他策略来估计有限元分析的误差。
估计误差有几个好处。首先,由于包含更小、数量更多的元素通常会提高精度,因此您可以对代码进行编程,使其在连续步骤中自动生成误差可能很大的区域中的更小元素。我们已经从 PDE 的数学分析中看到,应力在角和边缘附近增加得非常快。这种现象也使得这些区域的误差最大。无需手动在这些关键位置创建更精细的网格,就可以自动完成此步骤。
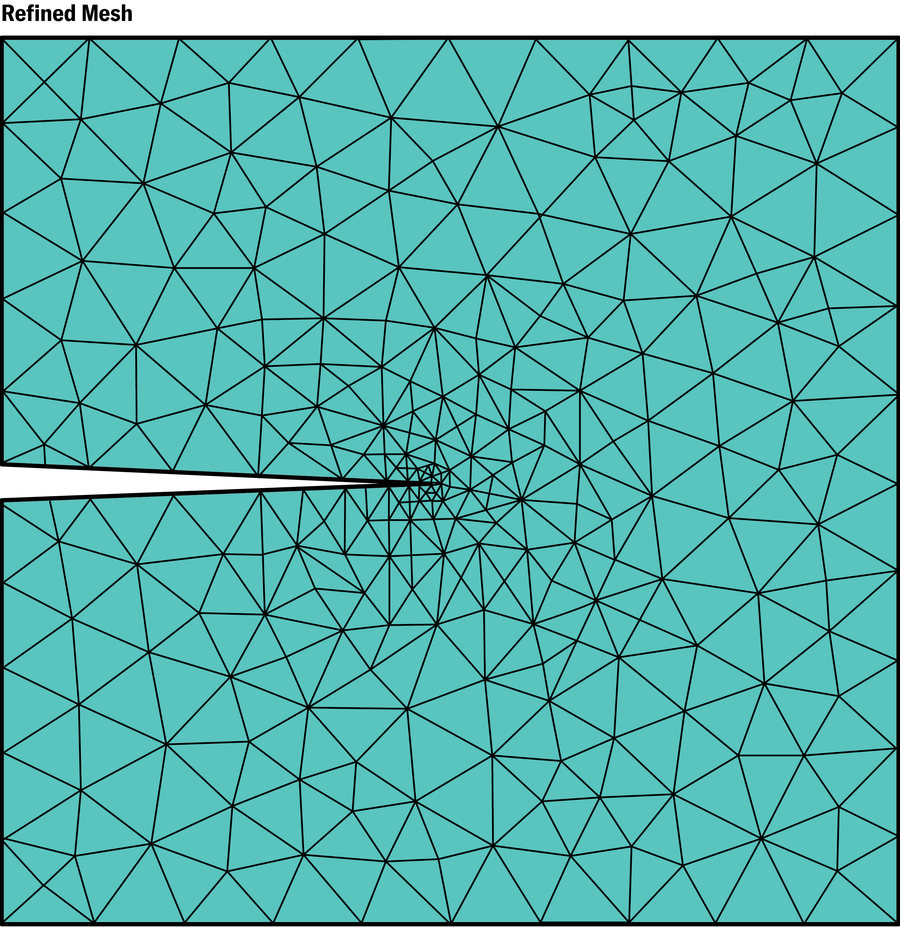
珍·克里斯蒂安森
其次,估计的总体误差可以帮助工程师衡量他们感兴趣的量的计算值的准确性,例如关键区域的应力强度或特定点的变形。工程师通常希望误差在一定范围内(从小于 2% 到 10%,具体取决于领域)。不幸的是,大多数算法会高估或低估误差,因此很难说它们提供的界限到底有多好。这方面仍然是一个活跃的研究领域。即便如此,如果使用误差估计,几乎肯定会提醒工程师注意他们挪威石油平台有限元模型的问题。
估计总体误差(即评估计算解的可靠性)的更好方法是使用有限元方法的不同理念:所谓的 p 细化,由圣路易斯华盛顿大学的工程师巴尔纳·萨博在 20 世纪 70 年代首次开发。通常提高精度的方法称为 h 细化,因为网格是通过减小典型元素的宽度(用 h 表示)来逐步细化的。对于 p 细化,我们始终坚持使用一个网格,但通过允许每个三角形以其他方式变形而不是始终保持平坦来提高精度。在第一步中,该方法允许任何三角形中的直线弯曲成抛物线,然后,逐步地,直线过渡到越来越复杂的曲线。这种修改为每个元素提供了越来越多的摆动空间,使其能够在每个步骤中更好地匹配解的形状。从数学上讲,此过程相当于增加底层多项式的次数 p,即用于表示不同类型曲线的代数公式。
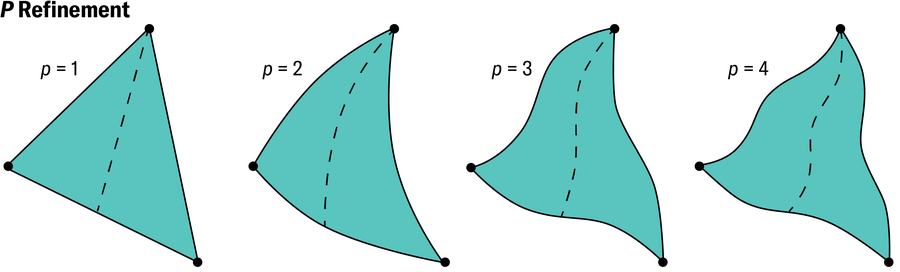
珍·克里斯蒂安森
正如巴布什卡和他的同事(包括我)所证明的那样,对于广泛的问题,p 细化比传统的 h 方法更快地收敛到 PDE 的精确解。我还帮助从数学上证明了 p 版本没有锁定问题,因此不需要用于 h 方法的任何修改。此外,事实证明,一系列摆动形状提供了一种简单可靠的方法来评估可靠性。
然而,令人沮丧的是,评估可靠性的 p 方法和 h 方法都没有在 20 世纪 70 年代至今使用的传统代码中发挥重要作用。原因可能是这些程序是在这些进步出现之前设计和在文化上根深蒂固的。在较新的工业代码中,StressCheck 程序基于 p 版本,并且确实提供了可靠性估计。
当有实验结果可供比较时,这种估计提供了进一步的好处:能够评估物理现实与用于对其建模的 PDE 之间的差异。如果您知道有限元分析是准确的,但您的总体误差仍然很大,那么您可以开始使用更复杂的模型,例如那些基于比例不再成立的物理学的模型,以弥合差距。理想情况下,任何基础数学模型都应通过与现实的此类比较来验证。
人工智能的出现很可能会改变计算机模拟的实践。首先,模拟将变得更加广泛可用。商业人工智能程序的一个共同目标是“普及化”有限元建模,向可能在该领域几乎没有内在专业知识的用户开放它。例如,自动化聊天机器人或虚拟助手可以帮助指导模拟。根据对此类助手进行培训的彻底程度,它们可能是一种宝贵的资源,特别是对于新手工程师而言。在最佳情况下,助手将响应以普通语言提出的查询,而不是需要技术性或格式化的措辞,并将帮助用户从通常令人眼花缭乱的可用元素阵列中进行选择,同时充分警惕在数学上可疑的修改。
人工智能可以发挥作用的另一种方式是生成网格,当由人工用户完成时,这可能会很昂贵,特别是对于角、裂缝尖端和其他特征附近所需的精细网格。数学家已经确定了在二维和三维此类区域中设计网格的精确规则。这些规则可能极其难以手动输入,但使用人工智能应该相当容易。未来的代码应该能够自动识别高应力区域并相应地划分网格。
一项更初步的工作涉及完全取代有限元分析,而是使用机器学习来求解 PDE。这个想法大致是训练一个神经网络来最小化残差 R,从而构建一系列越来越精确的载荷位移预测。由于裂缝尖端附近存在高局部应力,因此该方法在裂缝问题中的表现不佳,但研究人员发现,如果他们结合有关解的精确性质的信息(例如,通过使用孔德拉季耶夫的数学工作),则该方法可能可行。
在这些以及其他可能改变游戏规则的人工智能举措中,评估计算可靠性的这项绝对不起眼的任务(对于所有这些进步至关重要)尚未得到充分解决。利益相关者应参考 NASA 关于此类可靠性的要求。这些要求包括通过误差估计和其他方式证明,基本物理学对于正在建模的现实生活情况是有效的,并且诸如有限元解之类的近似值在 PDE 的真实解的可接受范围内。
NASA 最初将这些要求编纂成技术手册,以应对哥伦比亚号航天飞机灾难。未来人类专业知识和监督减少的前景应该同样是一个警钟。如果我们要信任人工智能提供的模拟结果,就需要内置可靠的可靠性保障措施。由于数学的进步,这些保障措施已经可用。我们需要将它们纳入数值模拟的各个方面,以在日益具有挑战性的世界中保持航空和其他工程事业的安全。

